↓跳过正文
简体中文

EN

简体中文

Quantization Introduction

··2194 字·5 分钟· loading · loading ·
NLP Transformer LLM AI Quantization
目录
AI Quantization - 这篇文章属于一个选集。
§ 1: DataType in AI
§ 2: 本文
§ 3: PTQ Methods for LLM

Introduction
#

LLMs的巨大模型规模和边缘设备的限制（主要是内存大小和带宽）给部署带来了显著挑战。

模型量化是指以较低的推理精度损失将连续取值（通常为float32或者大量可能的离散值）的浮点型权重近似为有限多个离散值（通常为int8）的过程。

通过以更少的位数表示浮点数据，可以有效降低 LLMs 对内存和带宽的需求，在一些低精度运算较快的处理器上可以增加推理速度。

Quantize Object
#

  • 权重，最常规的量化对象
  • 激活，activation 往往是占内存使用的大头，量化 activation 不仅可以减少内存占用，结合 weight 量化可以充分利用整数计算获得性能提升
  • KV Cache，有助于提高长序列生成的吞吐量
  • 梯度

LLM Quantization Example
# 

import numpy as np
np.random.seed(0)
# 生成维度为（5,5）的FP16格式的矩阵m1
m1 = np.random.rand(5, 5).astype(np.float16)
print(m1)
# 求scale
oldMax = np.max(m1)
scale = 127/oldMax
print(oldMax,scale)
# 量化为m2
m2 = np.round(scale * m1).astype(np.int8)
print(m2)
# 反量化为m3
m3 = (m2/scale).astype(np.float16)
print(m3)

现有 FP16 格式的权重矩阵m1:

[[0.549   0.7153  0.6025  0.545   0.4236 ]
 [0.646   0.4375  0.8916  0.964   0.3835 ]
 [0.7915  0.529   0.568   0.926   0.07104]
 [0.08716 0.02022 0.8325  0.7783  0.87   ]
 [0.9785  0.7993  0.4614  0.781   0.1183 ]]

量化为 INT8 格式的步骤：

  • 旧范围： FP16 格式中的最大权重值 - FP16 格式中的最小权重值 = 0.9785–0.07104
  • 新范围： INT8 包含从 -128 到 127 的数字。因此，范围 = 127-(-128)
  • 缩放比例(Scale)： 新范围中的最大值 / 旧范围中的最大值 = 127 / 0.9785 = 129.7884231536926
  • 量化值： Scale * 原始值, 四舍五入

m2:

[[ 71  93  78  71  55]
 [ 84  57 116 125  50]
 [103  69  74 120   9]
 [ 11   3 108 101 113]
 [127 104  60 101  15]]
  • 反量化： 量化值 / Scale

m3:

[[0.547   0.7163  0.601   0.547   0.4238 ]
 [0.647   0.4392  0.8936  0.963   0.3853 ]
 [0.7935  0.5317  0.5703  0.925   0.06934]
 [0.0848  0.02312 0.832   0.7783  0.8706 ]
 [0.9785  0.8013  0.4624  0.7783  0.1156 ]]

量化往往以 group 为单位，group 的划分对旧范围有影响

由于量化时产生了四舍五入和误差，导致反量化回到 FP16 格式后与原始数据略有误差

Asymmetry and symmetry quantization
#

量化的形式：

根据原始数据范围是否均匀，可以将量化方法分为线性量化和非线性量化。DL中的权重和激活值通常是不均匀的，因此理论上使用非线性量化导致的精度损失更小，但在实际推理中非线性量化的计算复杂度较高，通常使用线性量化。

线性量化的原理。假设 r 表示量化前的浮点数，量化后的整数 q 可以表示为：

$q=clip(round(r/s+z),q_{min},q_{max})$

其中，$round()$和$clip()$ 分别表示取整和截断操作，$q_{min}$和$q_{max}$表示量化后的上下限，$s$是数据量化的间隔，$z$是表示数据偏移的偏置。

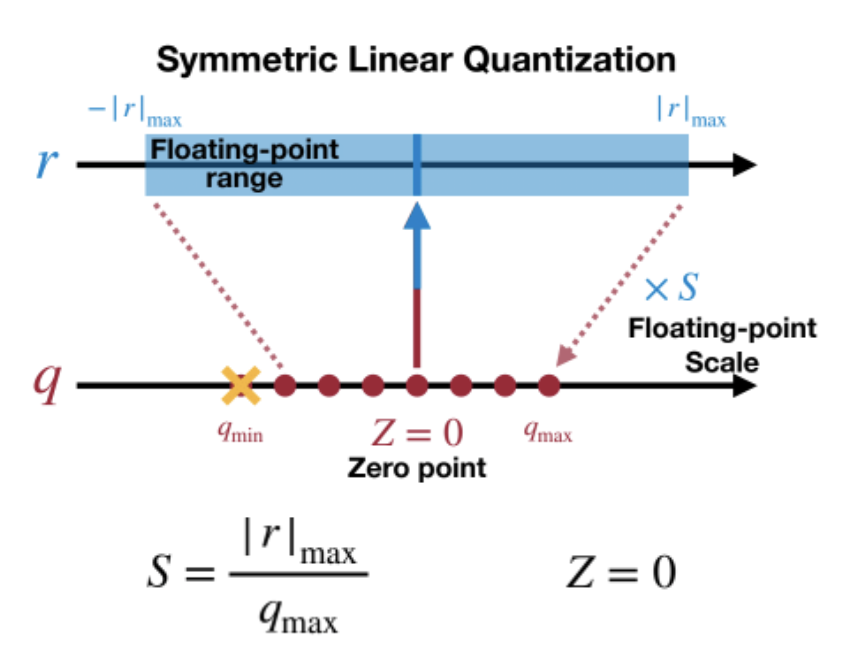
sym-quantize

当z=0时称为对称（Symmetric）量化，不为0时称为非对称（Asymmetric）量化。对于对称量化，原数值的 0 量化后仍然是 0，量化前后的数值都是以 0 为中点对称分布，但实际上有些数值的分布并不是左右对称的，比如 ReLU 激活后都是大于 0，这样会导致量化后 q 的范围只用到了一半，而非对称量化则解决了这个问题

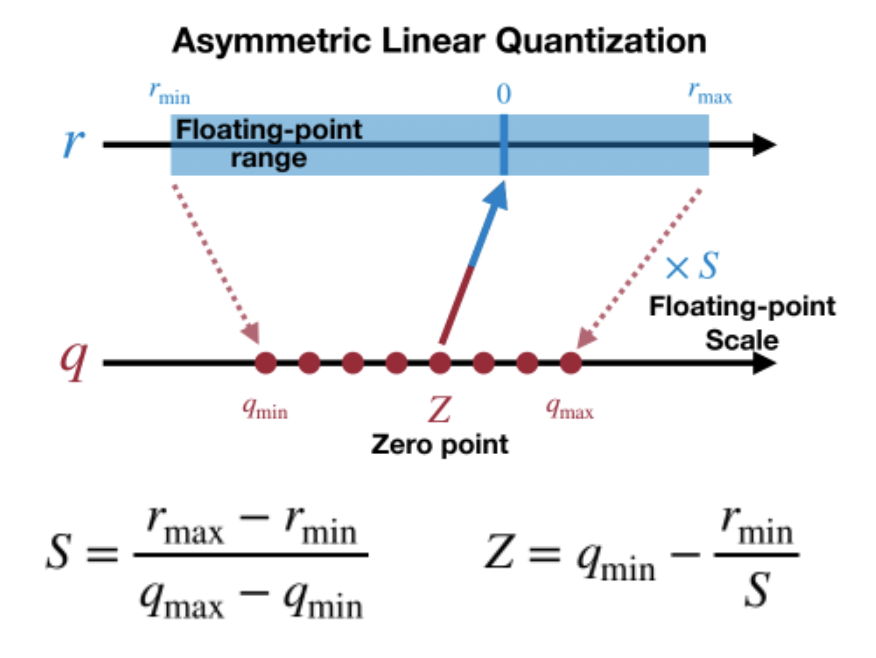
asym-quantize

非对称量化的 min、max 独立统计，Z 的值根据 r 的分布不同而不同，这样可以使 q 的范围被充分利用。

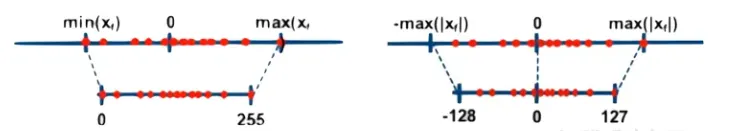
Asymmetry and symmetry quantization

对称量化可以避免量化算子在推理中计算z相关的部分，降低推理时的计算复杂度；非对称量化可以根据实际数据的分布确定最小值和最小值，可以更加充分的利用量化数据信息，使得量化导致的损失更低

量化的粒度
#

量化粒度指选取多少个待量化参数共享一个量化系数，通常来说粒度越大，精度损失越大。根据量化参数 s 和 z 的共享范围（即量化粒度），量化方法的粒度可以分为：

  • 逐层量化(per-tensor, per-layer)，是范围最大的粒度，以一层网络为量化单位，每层网络一组量化参数
  • 逐通道(per-token & per-channel 或 vector-wise quantization) 量化，以一层网络的每个量化通道为单位，每个通道单独使用一组量化参数
    • per-token：对激活来说，每行对应一个量化系数
    • per-channel：对权重来说，每列对应一个量化系数
  • 逐组量化(per-group, per-block, Group-wise)，粒度处于 per-tensor 和 per-channel 之间，每个group（如 K 行或 K 列）使用一组 s 和 z

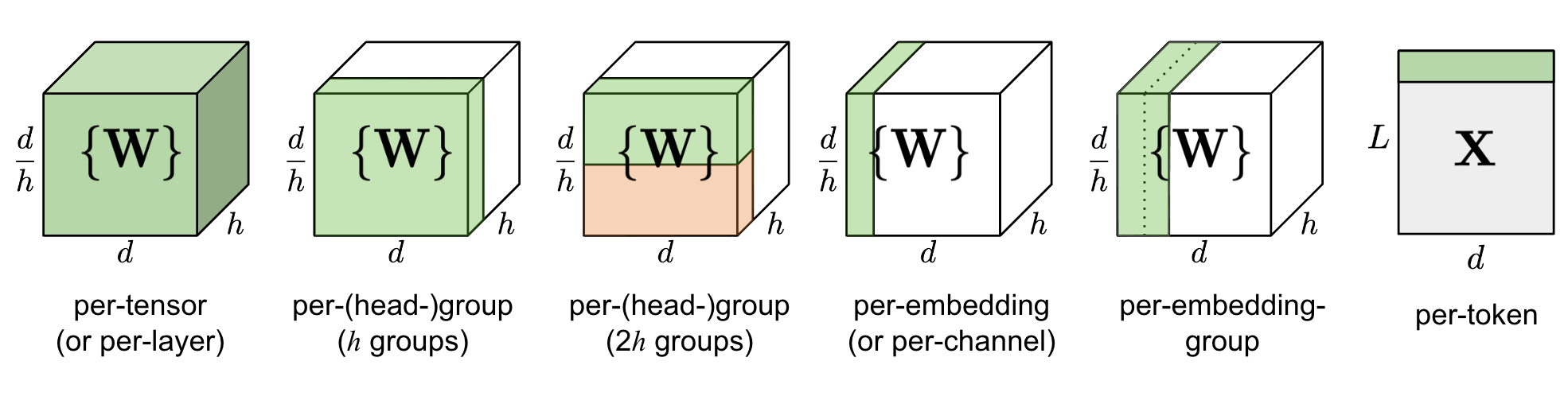
quantize 粒度

权重和激活可以选择不同的量化粒度。譬如权重用 per-tensor，激活用 per-token。并且对于激活分动态量化与静态量化

量化方法的分类
#

根据应用量化压缩模型的阶段，可以将模型量化分为：

  • 量化感知训练（Quantization Aware Training, QAT）：在模型训练过程中加入伪量化算子，通过训练时统计输入输出的数据范围可以提升量化后模型的精度，适用于对模型精度要求较高的场景；其量化目标无缝地集成到模型的训练过程中。这种方法使LLM在训练过程中适应低精度表示，增强其处理由量化引起的精度损失的能力。这种适应旨在量化过程之后保持更高性能
    • LLM-QAT
  • 量化感知微调（Quantization-Aware Fine-tuning，QAF）：在微调过程中对LLM进行量化。主要目标是确保经过微调的LLM在量化为较低位宽后仍保持性能。通过将量化感知整合到微调中，以在模型压缩和保持性能之间取得平衡
    • QLoRA
  • 训练后量化（Post Training Quantization, PTQ）：在LLM训练完成后对其参数进行量化，只需要少量校准数据，适用于追求高易用性和缺乏训练资源的场景。主要目标是减少LLM的存储和计算复杂性，而无需对LLM架构进行修改或进行重新训练。PTQ的主要优势在于其简单性和高效性。但PTQ可能会在量化过程中引入一定程度的精度损失。
    • LLM.int8()
    • GPTQ
    • AWQ

LLM 量化的挑战
#

  • 量化激活比量化权重更难（LLM.int8()表明，使用 INT8 甚至 INT4 量化 LLM 的权重不会降低准确性）
  • 异常值让量化激活更困难（激活的异常值比大多数激活值大 100 倍，使用 INT8 量化，大多数值将被清零）
  • 异常值持续存在于固定的通道中（固定通道存在异常值，并且异常值通道值较大）

LLM quantize challenge

Reference

AI Quantization - 这篇文章属于一个选集。
§ 1: DataType in AI
§ 2: 本文
§ 3: PTQ Methods for LLM