DataType in AI

Table of Contents

AI Quantization - This article is part of a series.

Part 1: This Article

Part 2: Quantization Introduction

Part 3: PTQ Methods for LLM

Data in Memory
#

Float 和 Double 类型的数据在内存中以二进制方式存储，由三部分组成：

符号位 S（Sign）: 0 代表正数，1 代表负数
指数位 E（Exponent）: 存储科学计数法中的指数部分，指数位越多，可表示的数值范围越大。
尾数位 M（Mantissa）: 存储尾数（小数）部分，尾数位越多，可表示的数值精度越高。

INT 类型只包括符号位和指数位，没有尾数位。

在计算机中，任何一个数都可以表示为 $1.xxx × 2^n$ 的形式，其中 n 是指数位，xxx 是尾数位，如 Float 9.125 在计算机中分别按照整数和尾数的二进制进行存储:

9 的二进制为 1001
0.125 的二进制为 0.001
9.125 表示为 1001.001，其二进制的科学计数法表示为 $1.001001 × 2^3$

DL 中模型的权重和激活通常由单精度浮点数(FP32)表示，如下图所示，FP32 包含1位符号位，8位指数位和23位尾数位，可以表示 1.18e-38 和 3.4e38 之间的值

DataTypes Comparation in AI
#

类型	bits	符号位	指数位	尾数位	范围	精度	原理	其他
FP32	32	1	8	23	$-3.4 \times 10^{38}$ ~ $3.4 \times 10^{38}$	$10^{-6}$		大部分CPU/GPU/深度学习框架中默认使用FP32
FP16	16	1	5	10	-65504 ~ 65504	$10^{-3}$		预训练LLM保存时默认使用的格式
TF32	19	1	8	10	$-3.4 \times 10^{38}$ ~ $3.4 \times 10^{38}$	$10^{-3}$	数值范围与FP32相同，精度与FP16相同	TF32(TensorFloat)是NV在Ampere架构GPU上推出的用于 TensorCore的格式，在A100 TF32 TensorCore的运算速度是V100 FP32 CUDACore的8倍
BF16	16	1	8	7	$-3.39 \times 10^{38}$ ~ $3.39 \times 10^{38}$	$10^{-2}$	数值范围与FP32一致，远大于FP16，但精度略低于FP16	BF16(brain floating point 16)由Google Brain提出，适合大模型训练，目前只适配于Ampere架构的GPU（A100）
Int32	32	1	31	0	$-2.15 \times 10^{9}$ ~ $2.15 \times 10^{9}$	1
Int16	16	1	15	0	-32768 ~ 32767	1
Int8	8	1	7	0	-128 ~ 127	1

使用pytorch验证数据：

import torch

print(torch.finfo(torch.float32))
# finfo(resolution=1e-06, min=-3.40282e+38, max=3.40282e+38, eps=1.19209e-07, smallest_normal=1.17549e-38, tiny=1.17549e-38, dtype=float32)

print(torch.finfo(torch.float16))
# finfo(resolution=0.001, min=-65504, max=65504, eps=0.000976562, smallest_normal=6.10352e-05, tiny=6.10352e-05, dtype=float16)

print(torch.finfo(torch.bfloat16))
# finfo(resolution=0.01, min=-3.38953e+38, max=3.38953e+38, eps=0.0078125, smallest_normal=1.17549e-38, tiny=1.17549e-38, dtype=bfloat16)

print(torch.iinfo(torch.int32))
# iinfo(min=-2.14748e+09, max=2.14748e+09, dtype=int32)

print(torch.iinfo(torch.int16))
# iinfo(min=-32768, max=32767, dtype=int16)

print(torch.iinfo(torch.int8))
# iinfo(min=-128, max=127, dtype=int8)

BF16 的优势：

设计思想是在不改变内存占用的情况下，用 1 / 10 倍的精度换取了 $10^{34}$ 倍的数值范围，只用 2 bytes 的内存，但数值范围与 4 bytes 的 FP32 相同
BF16 比 FP16 更适合深度学习。对于 DL，数值范围的作用远高于精度。因为在梯度下降时($w = w - \Delta w = w - grad * learningRate$)，grad 和学习率通常较小，因此必须使用能够表达较大范围的数据类型。使用 FP16时往往会出现 underflow：当数值小于 $− 6.55 × 10^4$ 时会被截断为 0 ，导致梯度无法更新。
BF16 与 FP32 的相互转换更容易。BF16 基本上可以看作成一个截断版的 FP32, 两者之间的转换是非常直接，相比于 FP16，BF16的电路实现更简单，可有效降低电路面积。

DataType Use Case
#

不用任务使用不同的数据类型
- 分类任务对数据类型比较不敏感，FP16 和 INT8 获得的精度差不多，一般可采用INT8
- NLP 任务以FP16为主
- 目标检测对数据类型比较敏感，以FP16为主
训练和推理的不同
- FP32 往往只是作为精度基线 (baseline)，比如要求使用 FP16 获得的精度达到 FP32 baseline 的 99% 以上。但 DL 训练，尤其是 LLM 训练，通常不会使用 FP32
- 训练往往使用 FP16, BF16 和 TF32，降低内存占用、训练时间和资源需求
- CV 推理以INT8为主， NLP 推理以FP16为主

DataType Conversion
#

GPU中的数据类型转换，FP32 转换为 FP16

强制把float转为unsigned long
尾数位：截取后23位尾数，右移13位，剩余10位
符号位：直接右移16位
指数位：截取指数的8位，先右移13位(左边多出3位不管了)，之前是0~255表示-127~128, 调整之后变成0~31表示-15~16，因此要减去（127-15=112再左移10位）

typedef unsigned short half;
half nvFloat2Half(float m)
{
    unsigned long m2 = *(unsigned long*)(&m);    
    unsigned short t = ((m2 & 0x007fffff) >> 13) | ((m2 & 0x80000000) >> 16) 
        | (((m2 & 0x7f800000) >> 13) - (112 << 10));           
    if(m2 & 0x1000) 
        t++;// 四舍五入(尾数被截掉部分的最高位为1, 则尾数剩余部分+1)
    half h = *(half*)(&t);// 强制转为half
    return h ;
}

FP16 转换为 FP32

float nvHalf2Float(half n)
{
    unsigned short frac = (n & 0x3ff) | 0x400;
    int exp = ((n & 0x7c00) >> 10) - 25;
    float m;
    if(frac == 0 && exp == 0x1f)
        m = INFINITY;
    else if (frac || exp)
        m = frac * pow(2, exp);
    else
        m = 0;
    return (n & 0x8000) ? -m : m;
}

Quantization in LLM
#

LLMs的巨大模型规模和边缘设备的限制（主要是内存大小和带宽）给部署带来了显著挑战。

模型量化是指以较低的推理精度损失将连续取值（通常为float32或者大量可能的离散值）的浮点型权重近似为有限多个离散值（通常为int8）的过程。

通过以更少的位数表示浮点数据，可以有效降低 LLMs 对内存和带宽的需求，在一些低精度运算较快的处理器上可以增加推理速度。

量化的对象：

权重，最常规的量化对象
激活，activation 往往是占内存使用的大头，量化 activation 不仅可以减少内存占用，结合 weight 量化可以充分利用整数计算获得性能提升
KV Cache，有助于提高长序列生成的吞吐量
梯度

LLM中的量化示例：

import numpy as np
np.random.seed(0)
# 生成维度为（5,5）的FP16格式的矩阵m1
m1 = np.random.rand(5, 5).astype(np.float16)
print(m1)
# 求scale
oldMax = np.max(m1)
scale = 127/oldMax
print(oldMax,scale)
# 量化为m2
m2 = np.round(scale * m1).astype(np.int8)
print(m2)
# 反量化为m3
m3 = (m2/scale).astype(np.float16)
print(m3)

现有 FP16 格式的权重矩阵m1:

[[0.549   0.7153  0.6025  0.545   0.4236 ]
 [0.646   0.4375  0.8916  0.964   0.3835 ]
 [0.7915  0.529   0.568   0.926   0.07104]
 [0.08716 0.02022 0.8325  0.7783  0.87   ]
 [0.9785  0.7993  0.4614  0.781   0.1183 ]]

量化为 INT8 格式的步骤：

旧范围： FP16 格式中的最大权重值 - FP16 格式中的最小权重值 = 0.9785–0.07104
新范围： INT8 包含从 -128 到 127 的数字。因此，范围 = 127-(-128)
缩放比例(Scale)：新范围中的最大值 / 旧范围中的最大值 = 127 / 0.9785 = 129.7884231536926
量化值： Scale * 原始值, 四舍五入

m2:

[[ 71  93  78  71  55]
 [ 84  57 116 125  50]
 [103  69  74 120   9]
 [ 11   3 108 101 113]
 [127 104  60 101  15]]

反量化：量化值 / Scale

m3:

[[0.547   0.7163  0.601   0.547   0.4238 ]
 [0.647   0.4392  0.8936  0.963   0.3853 ]
 [0.7935  0.5317  0.5703  0.925   0.06934]
 [0.0848  0.02312 0.832   0.7783  0.8706 ]
 [0.9785  0.8013  0.4624  0.7783  0.1156 ]]

量化往往以 group 为单位，group 的划分对旧范围有影响

由于量化时产生了四舍五入和误差，导致反量化回到 FP16 格式后与原始数据略有误差

Asymmetry and symmetry quantization
#

量化的形式：

根据原始数据范围是否均匀，可以将量化方法分为线性量化和非线性量化。DL中的权重和激活值通常是不均匀的，因此理论上使用非线性量化导致的精度损失更小，但在实际推理中非线性量化的计算复杂度较高，通常使用线性量化。

线性量化的原理。假设r表示量化前的浮点数，量化后的整数q可以表示为：

$q=clip(round(r/s+z),q_{min},q_{max})$

其中，$round()$和$clip()$ 分别表示取整和截断操作，$q_{min}$和$q_{max}$表示量化后的上下限，$s$是数据量画的间隔，$z$是表示数据偏移的偏置，当z=0时称为对称（Symmetric）量化，不为0时称为非对称（Asymmetric）量化

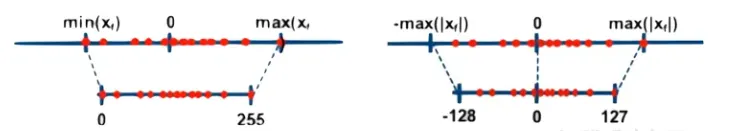
对称量化可以避免量化算子在推理中计算z相关的部分，降低推理时的计算复杂度；非对称量化可以根据实际数据的分布确定最小值和最小值，可以更加充分的利用量化数据信息，使得量化导致的损失更低

量化的粒度：

根据量化参数sss和zzz的共享范围（即量化粒度），量化方法可以分为逐层量化（per-tensor）、逐通道（per-token & per-channel 或者 vector-wise quantization ）量化和逐组量化（per-group、Group-wise）。

Reference

AI Quantization - This article is part of a series.

Part 1: This Article

Part 2: Quantization Introduction

Part 3: PTQ Methods for LLM

类型	bits	符号位	指数位	尾数位	范围	精度	原理	其他
FP32	32	1	8	23	\(-3.4 \times 10^{38}\) ~ \(3.4 \times 10^{38}\)	\(10^{-6}\)		大部分CPU/GPU/深度学习框架中默认使用FP32
FP16	16	1	5	10	-65504 ~ 65504	\(10^{-3}\)		预训练LLM保存时默认使用的格式
TF32	19	1	8	10	\(-3.4 \times 10^{38}\) ~ \(3.4 \times 10^{38}\)	\(10^{-3}\)	数值范围与FP32相同，精度与FP16相同	TF32(TensorFloat)是NV在Ampere架构GPU上推出的用于 TensorCore的格式，在A100 TF32 TensorCore的运算速度是V100 FP32 CUDACore的8倍
BF16	16	1	8	7	\(-3.39 \times 10^{38}\) ~ \(3.39 \times 10^{38}\)	\(10^{-2}\)	数值范围与FP32一致，远大于FP16，但精度略低于FP16	BF16(brain floating point 16)由Google Brain提出，适合大模型训练，目前只适配于Ampere架构的GPU（A100）
Int32	32	1	31	0	\(-2.15 \times 10^{9}\) ~ \(2.15 \times 10^{9}\)	1
Int16	16	1	15	0	-32768 ~ 32767	1
Int8	8	1	7	0	-128 ~ 127	1

Data in Memory #

DataTypes Comparation in AI #

DataType Use Case #

DataType Conversion #

Quantization in LLM #

Asymmetry and symmetry quantization #