FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness
与标准 attention 相比,Flash Attention 有以下三点特点:
- 运算速度更快 (Fast)
- 更节省显存 (Memory-Efficient)
- 计算结果相同 (Exact)
FlashAttention 目的不是节约 FLOPs,而是减少对HBM的访问。它没有改变原有的计算公式,整体计算复杂度并未降低。
Self-attention #
GPU中存储单元主要有 HBM 和 SRAM:HBM 容量大但是访问速度慢,SRAM容量小却有着较高的访问速度。例如:A100 GPU有40-80GB的HBM,带宽为1.5-2.0TB/s;每108个流式多核处理器各有192KB的片上SRAM,带宽估计约为 19TB/s。可以看出,片上的SRAM比HBM快一个数量级,但尺寸要小许多数量级。
当输入序列(sequence length)较长时,Transformer的计算过程缓慢且耗费内存,这是因为 self-attention 的 time 和 memory complexity 会随着 sequence length 的增加成二次增长。
标准 Attention 的计算过程: $$ S=Q K^T \in \mathbb{R}^{N \times N} $$ $$ P=\operatorname{softmax}(S) \in \mathbb{R}^{N \times N} $$ $$ O=P V \in \mathbb{R}^{N \times N} $$
softmax 计算:
$$m(x):=\max _i x i$$ $$f(x):=\left[e^{x_1-m(x)} \ldots e^{x_B-m(x)}\right]$$ $$\ell(x):=\sum_i f(x)_i$$ $$\operatorname{softmax}(x):=\frac{f(x)}{\ell(x)}$$
softmax 伪代码:
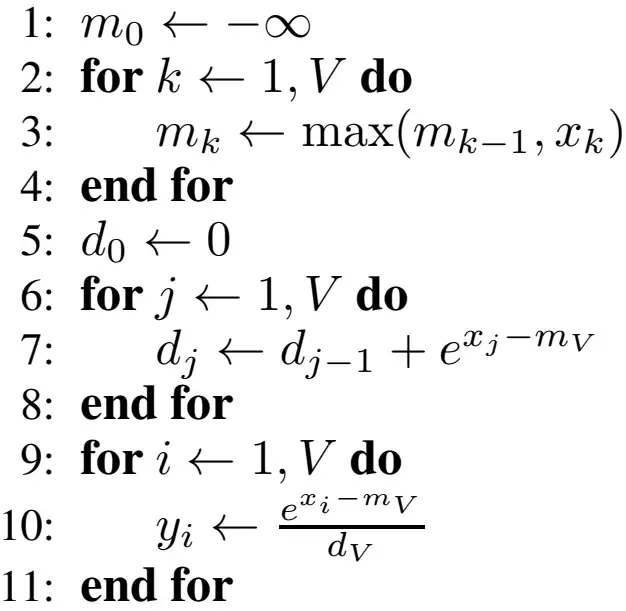
softmax 函数需要三个循环,第一个循环计算数组的最大值,第二个循环计算 softmax 的分母,第三个循环计算 softmax 输出。
复杂度分析:
- 读取Q,K,写入\(S=QK^T\),内存访问复杂度\(O(Nd+N^2)\)
- 读取S,写入\(P=softmax(S)\),内存访问复杂度\(O(N^2)\)
- 读取V和P,写入\(O=PV\),内存访问复杂度\(O(Nd+N^2)\)
综上,self-attention 的中间结果 𝑆, 𝑃 通常需要通过高带宽内存(HBM)进行存取,self-attention 的 HBM 访问复杂度\(O(Nd+N^2)\),对 HBM 的重复读写是主要瓶颈。要解决这个问题,需要做两件事:
- 在不访问整个输入的情况下计算 softmax
- 不为反向传播存储大的中间 attention 矩阵(\(N^2\))
FlashAttention V1 #
FlashAttention-V1 提出了两种方法来解决上述问题:tiling 和 recomputation。
- tiling - 注意力计算被重新构造,将输入分割成块,并通过在输入块上进行多次传递来递增地执行softmax操作。
- recomputation - 存储来自前向的 softmax 归一化因子,以便在反向中快速重新计算芯片上的 attention,这比从HBM读取中间矩阵的标准注意力方法更快。可以把它看作基于 tiling 的特殊的 gradient checkpointing
FlashAttention 设计了一套分而治之的算法,将大的矩阵切块加载到SRAM,计算每个分块的m和l值。利用上一轮m和l结合新的子块迭代计算,最终算出整个矩阵的数值。整个过程不用存储中间变量S和P矩阵,因此节省了效率。
分块的 softmax 计算(假设分2块并行计算):
$$m(x)=m\left(\left[x^{(1)} x^{(2)}\right]\right)=\max \left(m\left(x^{(1)}\right), m\left(x^{(2)}\right)\right) $$ $$f(x)=\left[e^{m\left(x^{(1)}\right)-m(x)} f\left(x^{(1)}\right) \quad e^{m\left(x^{(2)}\right)-m(x)} f\left(x^{(2)}\right)\right] $$ $$\ell(x)=\ell\left(\left[x^{(1)} x^{(2)}\right]\right)=e^{m\left(x^{(1)}\right)-m(x)} \ell\left(x^{(1)}\right)+e^{m\left(x^{(2)}\right)-m(x)} \ell\left(x^{(2)}\right) $$ $$\operatorname{softmax}(x)=\frac{f(x)}{\ell(x)}$$
分块的 softmax 伪代码:
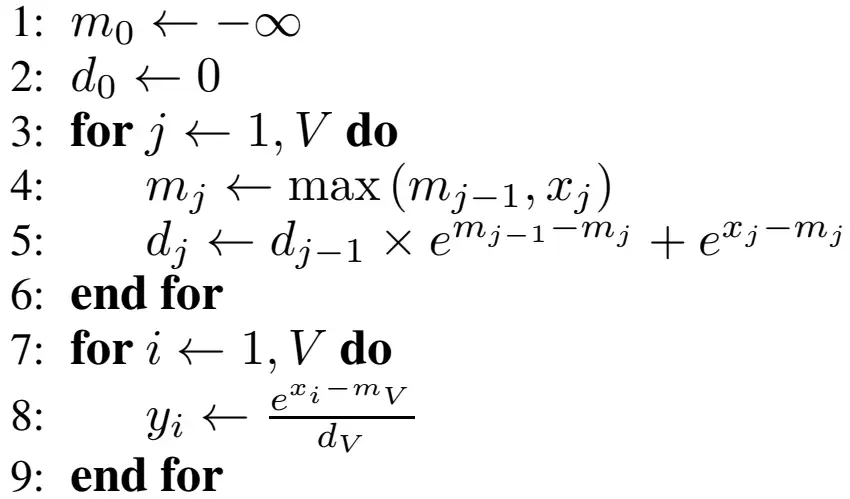
在第一个循环中同时对最大值\(m\)以及 softmax 的分母\(d\)进行更新,从而减少了一个循环。通过 tiling 的方式,softmax 的循环数从三个减到了两个,从而可以降低内存消耗。
flashattention 伪代码:

中间变量:\(O_i\)(最终乘积)、\(l_i\)(softmax的分母,即累加和)、\(m_i\)(遍历到当前块为止的最大值),再也不用保存全部的S和P了。
由于重新计算导致 FLOPs 增加,但是由于大量减少HBM访问,FlashAttention 运行速度更快
FlashAttention的 FLOPs 为 \(𝑂(𝑁^2𝑑)\),除了 input 和 output,额外需要的内存为 \(𝑂(𝑁)\), 对HBM访问的次数为 \(𝑂(𝑁^2𝑑^2𝑀^{−1})\), 其中 M 为SRAM的大小,当 \(M=O(Nd)\)时,对HBM访问的次数为\(O(Nd)\), 远远小于标准 Attention 的 \(O(Nd+N^2)\)
PyTorch 2.0已将 FlashAttention 集成到官方库中,可以直接调用 torch.nn.functional.scaled_dot_product_attention
总结 #
FlashAttention V1:
- 通过切块技术减少了内存访问次数,提高了计算速度和内存利用率。
- 内存访问复杂度为 \(𝑂(𝑁^2𝑑^2𝑀^{−1})\), 比标准 Attention 的 \(O(Nd+N^2)\)更高效
Reference:
